问题描述

汉诺塔：有三根柱子，第一根柱子上面从上到下依次摆放着n个从小到大的圆盘，第二和第三根柱子是空的，遵循一定的游戏规则，将第一根柱子上面的圆盘移动到第三根柱子上.游戏规则就是：移动过程中可以借助第二根柱子，但是始终不能够将大的盘子放在小的盘子之上。

简单的摆法如下图所示：

解法

解决汉诺塔问题，最常见的也是最容易想到的就是递归分解问题，
假设三根柱子分别是A,B,C，需要将A上的盘子移动到C上

情况1、如果A上只有一个盘子，直接移动到C上。

情况2、如果A上有两个盘子，先将A上面的小的移动到B上(使用了C作为辅助)，再将大的移动到C上，最后将B上的盘子移动到C上。

情况3、如果A上有个三个盘子，(先将最小的移动到C上，第二小的移动到B上，再将C上的最小的移动到B上)^[1]，(然后将A上留下的最大的移动到C上)^[2]，(然后将B上的最小的移动到A上)^[3]，然后将B上剩下的一个移动到C上，最后将A上的最小的移动到C上。

让我们来看看情况3、^[1]处使用了C作为辅助的柱子，先将A上的前2个移动到了B上(这里就是情况2)，^[2]处直接将A上的，最后一个移动到了C上(这里就是情况1)，最后^[3]处是用了A作为辅助的柱子，将B上的东西移动到了C上(这里就是情况2，不同的是辅助的柱子不一样了)。

总结：当有n个盘子的时候，首先将上面的n-1个借助C移动到B上，然后将A上的最后一个移动到C上，然后再借助A将B上的n-1个移动到C上。

代码

# -*- coding: cp936 -*-  
def hannoi(n,A,B,C):  
    if n==1:  
        print(A," ----> ",C)  
    else:  
        hannoi(n-1,A,C,B)#将前n-1个盘子从 A 移动到 B 上  
        print(A," ----> ",C)#将最底下的一个胖子从 A 移动到 C 上  
        hannoi(n-1,B,A,C)#将 B 上的n-1个盘子移动到 C 上  
n=int(input("请输入汉诺塔的层数："))  
hannoi(n,"A","B","C")

汉诺塔之python

问题描述

解法

代码

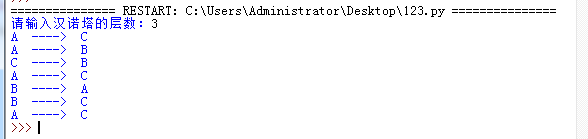
结果